Polygenic or Multifactorial Inheritance
Authors
INTRODUCTION
Neither chromosomal abnormalities nor single gene (Mendelian) inheritance can explain all aspects of heritability. Heritability of anatomic and physiologic variation (e.g., stature) is one example, and heritability of birth defects limited to a single organ system is another. Yet it is obvious that relatives often resemble one another in physical appearance. It is also obvious that most congenital anomalies show heritable tendencies, but not to the extent that a single mutant gene could be postulated as causative. For example, after the birth of one child with congenital cardiac defects, the likelihood is 1–4% that any subsequent progeny will be similarly affected. A parent with a cardiac anomaly has a risk for his/her offspring being similarly affected. This risk is greater than the incidence in the population, but much less than that expected on the basis of a single recessive or dominant gene (25% and 50%, respectively). Inheritance consistent with the above is best explained on the basis of the cumulative effect of several genes or alleles, producing a continuous variation of genotypes in the general population. This mode of inheritance (polygenic/multifactorial) is the subject of this chapter, which inevitably reflects the author's previous discussions on the subject.1
COULD SHARED ENVIRONMENTAL FACTORS ALONE EXPLAIN FAMILIAL AGGREGATES?
One possible explanation for familial aggregates is common exposure to environmental factors; however, such a postulate (shared environmental factors) usually proves unsustainable. Given differences of several decades, it is unlikely that parents and offspring will be exposed to exactly the same deleterious agents. Only if more than one generation is raised in the same house is the hypothesis worthy of serious discussion. Moreover, even if multiple siblings are similarly exposed to a causative agent, one would expect all siblings to be affected rather than only a minority.
Genetic factors are far more plausible. Data from twin studies offer the most overt evidence for existence of genetic factors. Monozygotic (MZ) twins are much more likely to be concordant for any given anomaly (or adult-onset disorder) than are dizygotic (DZ) twins. MZ and DZ twins are generally exposed to the same intrauterine environmental factors; thus, genetic factors need to be invoked.
POLYGENIC INHERITANCE AND CONTINUOUS GENOTYPIC VARIATION
Familial resemblances for anatomic characteristics are influenced by not one but several genes that cumulatively can produce enough genotypes to mimic a normal distribution in the general population. To illustrate this, let us consider the result of sequentially increasing the number of genes influencing a given trait.
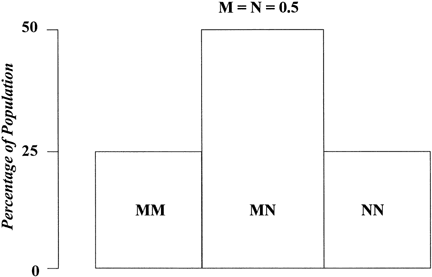
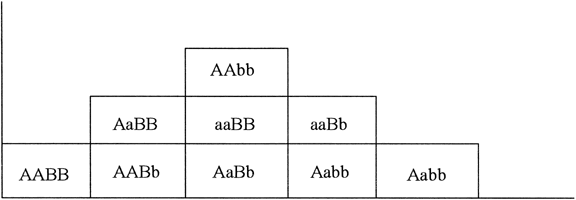
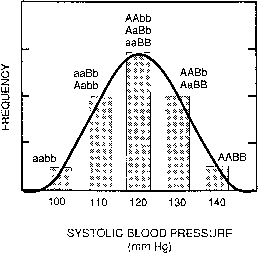
Suppose only one gene controls a given trait and that this gene has only two alleles (A,a). If the frequency of allele A equals the frequency of allele a, 25% of the population is AA based on Hardy-Weinberg equilibrium: p = q = 0.5; p2 = q2 = 0.25; the frequency of aa is also 25%. Aa accounts for 50% (2 pq = 0.50) (Fig. 1). Now suppose that not one but two genes influence a given trait. At the second locus, alleles B and b exist. Nine genotypes are now possible: AABB, AABb, AAbb, AaBB, AaBb, Aabb, aaBB, aaBb, and aabb (Table 1). The population will contain nine phenotypic classes if alleles A, B, a, and b each exert dissimilar influences. If alleles A and B or a and b exert equal effect, only five phenotypic classes exist (Fig. 2). As the number of genes controlling a trait increases, the number of genotypes in the population increases geometrically. If three genes exist, each with two alleles, there are 27 genotypic classes (3n). Even more genotypes exist per locus if the locus has more than two alleles. If there is one locus with three alleles per locus, there are six genotypes (Table 2). If there are two genes, each with three alleles, there are 36 genotypes (see Table 2).
Table 1. Relationship between numbers of genes controlling a trait and numbers of genotypes in a population
No. of loci | Alleles | Genotypes | No. of genotypes (formula) |
1 | (M,N) | MM MN NN | 3 (31) |
2 | (M,N;R,S) | MMRR MMRS MMSS MNRR MNRS MNSS NNRR NNRS NNSS | 9 (32) |
N | (2 alleles per locus) |
| 3n |
Genotypes listed assume two alleles per locus, each of which exerts a differential phenotypic effect.
Table 2. Relationship between numbers of genes controlling a trait and number of genotypes in a population
No. of loci | Alleles | Genotypes | No. of genotypes (formula) |
1 | (M,N,O) | MM MN MO NN NO OO | 6 (61) |
2 | (M,N,O;P,Q,R) |
| 36 (62) |
N | (3 alleles per locus) |
| 6n |
Genotypes listed assume three alleles per locus.
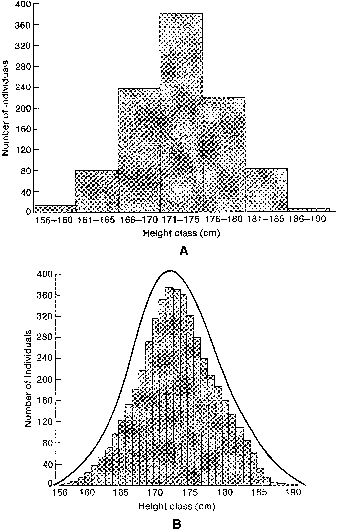
If one histographically represents the number of individuals in each genotypic class, a normal distribution is increasingly approximated as more genotypes exist. With only a few genes, 27 or 36 different genotypes can be produced (see Tables 1 and 2), enough to mimic continuous variation. Figure 3 shows this concept in a different way. If one stratifies heights in the general population into increasingly smaller intervals (1 cm vs 5 cm), histographic representation of the phenotypes better fits the normal distribution. Figure 4 illustrates this for pathologic traits, the assumption being that only two genes, each with two alleles, determine blood pressure. Table 3 lists several physiologic or anatomic variables for which polygenic inheritance with continuous variation can plausibly be assumed. See Simpson and Elias1 for additional examples.
Table 3. Anatomic and physiologic traits showing continuous variation and presumably inherited in polygenic fashion
| Age of menarche |
| Age of natural menopause (oocyte pool) |
| Blood pressure during pregnancy |
| Gestational length |
| Height |
| Pelvic shape |
| Resistance against pelvic relaxation |
| Responsiveness to medications |
| Weight (tendency toward obesity) |
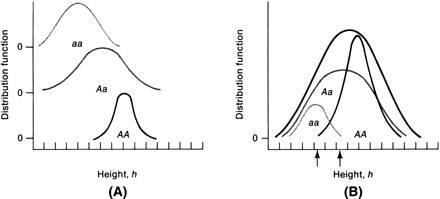
Ostensibly normal distribution of phenotypes in the population can also be explained by several alleles or several genes having nonoverlapping distributions. If only the phenotype is measured, not individual alleles or genes, a normal distribution is seen in the general population (Fig. 5).
Applying the principles of polygenic inheritance explains why offspring usually, but do not always, reflect parental phenotype. Height can serve as a hypothetical example, for it is well established that a child's height correlates with his/her midparental height, corrected for sex. Suppose height is governed by three genes, each with only two alleles (A,a; B,b; C,c). Each upper case allele (A, B, C) might confer an additional 3 inches in height above some threshold, hypothetically here 60 inches for males and 54 inches for female. Each lower case allele (a, b, c) might contribute nothing above the threshold. Thus, a male of genotype AaBBcC would be 72 inches tall [60 + (4 × 3) = 72]; a female of genotype AaBbCc would be 63 inches tall [54 + (3 × 3) = 63]. On average, one would expect the male parent in the above example to contribute 2 upper case alleles (4/2 = 2) and the female parent 1.5 (3/2 = 1.5). Thus, a child will on average inherit 3.5 upper case alleles and thus approximate parental heights. Offspring, however, could inherit between 1 and 6 upper case alleles and, hence, show heights ranging from 63 to 78 inches in males and 57 to 72 inches in females. The likelihood of various genotypic possibilities producing these extremes is illustrated in Table 4.
Table 4. Hypothetical example showing probability of an uncommon genotype (tall stature or short stature) arising from a mating involving two parents of average height
| Parental height (inches) | ||||
(1) Parental genotypes and height |
| Male | Aa BB Cc | 72 | |
|
| Female | Aa Bb Cc | 63 | |
| Offspring height (inches) | ||||
| Genotype in offspring | Probability of genotype arising | Male | Female | |
(2) Probabilities of selected genotypes in offspring and expected height | Aa Bb Cc | 1/2 × 1/2 × 1/2 = 1/8 | 69 | 63 | |
AA BB CC | 1/4 × 1/2 × 1/4 = 1/32 | 78 | 72 | ||
aa Bb cc | 1/4 × 1/2 × 1/4 = 1/32 | 63 | 57 | ||
Baseline height threshold (inches): Males: 60; Females: 54.
Calculation of height above threshold: For each A, B, or C allele add 3; for each a, b, or c allele add 0.
Murphy and Chase,2 Griffiths and associates,3 Vogel and Motulsky,4 and Lynch and Walsh5 provide more detailed and mathematically substantiated discussion of the underlying basis of polygenic inheritance.
MULTIFACTORIAL VERSUS POLYGENIC
The term polygenic inheritance is typically used synonymously with continuous variation, but the latter may theoretically result from presence of interaction between a single locus and environmental factors. The environmental factor would presumably need to be almost ubiquitous, but this is not impossible. Examples might include a hazardous waste site, common workplace exposure of low toxicity, or frequently consumed drug (e.g., aspirin) or toxin (e.g., alcohol or cigarette smoke). If environmental as well as genetic factors influence a trait, the term multifactorial is more appropriate.
In humans, one probably cannot distinguish polygenic from multifactorial inheritance, although comparisons between MZ and DZ twins theoretically permit such a distinction. Some geneticists often apply the term polygenic to any trait whose inheritance is complex. Others apply the term multifactorial equally indiscriminately. To this author, it is preferable to invoke the term polygenic/multifactorial, given that the genetic complexities in humans have not been precisely elucidated.
DISCONTINUOUS VARIATION IN POLYGENIC/MULTIFACTORIAL INHERITANCE
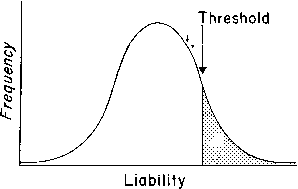
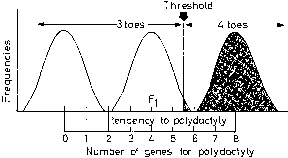
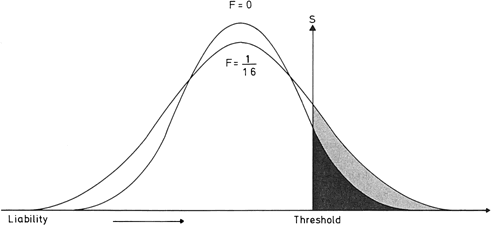
In discontinuous variation, the population consists of two discrete groups. An individual is either affected (e.g., cleft palate) or not. Either an infant has anencephaly or he/she does not. There is no continuum in the population. Table 5 lists several anatomic defects in which discrete affected/unaffected groups exist. In those malformations, the recurrence risk for first-degree relatives is 1–5%. Heritable factors of a polygenic/multifactorial nature must exist, or the recurrence risk would not exceed population incidence, which is usually 0.1% or less. To explain the dichotomy (discontinuity) on a polygenic/multifactorial model, one can postulate a threshold beyond which the accrued genetic liability for developing a specific trait becomes so great that a malformation is or can be manifested (Fig. 6). The validity of this concept has been appreciated for at least 70 years. Figure 7 shows results of a 70-year-old landmark breeding experiment in which Wright6 found a threshold effect for polydactyly (four toes) in guinea pigs.
Table 5. Polygenic/multifactorial traits showing discontinuous variation
| Cardiac defects (most types) |
| Cleft lip (alone) |
| Cleft lip, with or without cleft palate |
| Diaphragmatic hernia |
| Hip dislocation |
| Hypospadias (penile or glandular) |
| Incomplete Müllerian fusion |
| Limb reduction defect (most forms) |
| Müllerian aplasia |
| Neural tube defects (anencephaly, spina bifida, encephalocele) |
| Omphalocele |
| Posterior urethral valves |
| Renal agenesis |
| Talipes equinovarus |
This mode of inheritance can be assumed if the malformation is not accompanied by anomalies in other organ systems.
|
Phenotypically normal parents delivering a child with a polygenic/multifactorial trait (anomaly) can be assumed to have genetic liabilities nearer the threshold than others in the general population. The small arrows in Figure 6 connote probable genotypes of unaffected parents who have a child with a polygenic/multifactorial trait. Their genotypes are probably nearer the threshold, explaining the higher risk for recurrence in subsequent progeny. By similar reasoning, a parent with a polygenic/multifactorial trait has a 1–5% risk for an affected offspring. The risk is less for second- and third-degree relatives than for first-degree relatives because their genotypes are further from the threshold, closer to the mean, for the general population (Fig. 8).
The threshold model becomes highly plausible biologically if “liability” on the abscissa is replaced with “rate of embryonic growth”. If growth is too slow to permit a key embryonic step from being accomplished by a certain time interval, anomalous development may result. For example, if the paired palatine shelves reach the midline prior to a certain day of development, fusion occurs to form the secondary palate. After that day, the shelves are too widely separated to fuse, resulting in cleft palate. In a polygenic model, the inherited factors (genes) might include velocity of growth, size of the mandible and tongue, and rapidity of palatine migration. Similar reasoning could apply to incomplete Müllerian fusion or Müllerian aplasia.
CRITERIA FOR POLYGENIC/MULTIFACTORIAL INHERITANCE
Certain characteristics are expected of a trait inherited in polygenic/multifactorial fashion and showing discontinuous variation. Traits fulfilling most or all of these criteria can be deduced to be inherited in polygenic/multifactorial fashion, with recurrence risks of 1–5% even in the absence of empiric data. These disorders usually have an incidence of about 1 per 1000 live births. They typically involve a single organ system or embryologically related organ systems.
Recurrence risk as function of relatedness
In polygenic/multifactorial inheritance, frequency of similarly affected co-twins (concordance) is higher among MZ than DZ twins. Unlike expectations for Mendelian traits, however, discordantly affected co-twins are observed among MZ twins. Table 6 contrasts concordance in MZ and DZ twins for Mendelian versus polygenic/multifactorial inheritance.2
Table 6. Concordance in twins for various modes of inheritance
| Monozygotic (%) | Dizygotic (%) |
Autosomal dominant | 100 | 50 |
Autosomal recessive | 100 | 25 |
Polygenic/multifactorial | 50–75 | 5–10 |
Environmental (exclusively) | ~100 | ~100 if monochorionic <100 if dichorionic |
For DZ and nontwin siblings, recurrence risk approximates the square root of the incidence. Thus, the rarer the trait, the lower the recurrence risk. For more distant relatives, recurrence risk decreases. As the degree of relatedness decreases, recurrence risk for relatives decreases more rapidly than that observed for autosomal dominant traits.
It is often not appreciated is that consanguineous unions carry increased risks for polygenic/multifactorial traits (Fig. 9). The effect is less pronounced than for autosomal recessive traits. Nonetheless, there are increased risks whenever a common ancestor confers identity by descent of certain alleles, normal or abnormal (Mendelian or polygenic).
Recurrence risk as function of prior offspring
Unlike Mendelian inheritance, recurrence risk increases empirically after more than one progeny is affected. The risk rarely approaches the 25% expected for recessive traits or the 50% expected for dominant traits; however, after three affected offspring, the risk may be so high (15–20%) that one cannot exclude autosomal recessive inheritance in that family.
Recurrence risk by severity
The more serious the defect, the higher the recurrence risk. Bilateral cleft palate carries a higher recurrence risk than unilateral cleft palate. Long-segment aganglionosis (Hirschsprung disease) carries a higher recurrence risk than short-segment aganglionosis. Complete uterine didelphysis with vaginal septum should confer a higher recurrence risk than acute or subseptate uterus. Presumably a more severe phenotype indicates genotypic liability further beyond the threshold than is necessary to manifest a less severe trait. In turn, the distribution of genotypes in first-degree relatives (parents) would be more likely to be displaced to the right (i.e., further from the mean of the general population and perhaps just short of the threshold).
Recurrence risk by sex
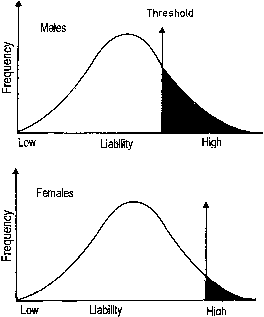
If the trait occurs more frequently among members of one sex, the risk of recurrence is higher if the proband (index case) is of the less frequently affected sex. The prototypic example is pyloric stenosis, which occurs more frequently in men. Thus, the recurrence risk is higher if the proband is female (Table 7). The converse is true for congenital hip dislocation, in which women are more frequently affected. The assumption is that the threshold must be displaced further to the right in the less frequently affected sex, thus resulting in a lower recurrence risk. Figure 10 illustrates this concept.
Table 7. Differences in recurrence risks for pyloric stenosis
| Third-degree relatives | |||||||
| First-degree relatives | Second-degree relatives | Male | Female | ||||
Index case | Brother (%) | Sister (%) | Son (%) | Daughter (%) | Nephew (%) | Niece (%) | Cousin (%) | Cousin (%) |
Male | 2.17 | 2.07 | 6.42 | 2.55 | 2.16 | 0.47 | 0.57 | 0.29 |
Female | 10.89 | 8.91 | 22.95 | 11.48 | 6.67 | 1.28 | 0.81 | 0.2 |
Pyloric stenosis is used as an illustrative polygenic/multifactorial trait in which one sex (male) is more frequently affected than the other (female).
(Data from Carter CO: The inheritance of congenital pyloric stenosis. Br Med Bull 17: 251, 1961.)
PROPORTION OF GENETIC CONTROL IN MULTIFACTORIAL TRAITS: HERITABILITY (h2) AND GENETIC DETERMINATION (H)
In theory, the exact proportion of genetic and nongenetic factors responsible for multifactorial traits (as strictly defined) can be determined. This proportion is termed heritability (h2). The specific part of variation being estimated quantitatively is additive genetic variation. Additive factors are those that can always be transmitted from generation to generation. The concept of heritability is applied in plant and animal breeding, species in which matings and environment may be controlled.
That heritability measures additive genetic variation means excluding genetic variation independent of dominance or epistasis. Dominance involves interaction between alleles at a single locus, whereas epistasis involves interaction of alleles at different loci. Dominance and epistasis are not additive because their contributions are determined again each successive generation. By contrast, additive factors are always transmitted from generation to generation.
In humans, attempts have been made to calculate heritability for continuous variables such as height or blood pressure. Usually twin studies are used to make estimates; however, in human populations neither matings nor environment can be controlled. Thus, heritability calculations can represent only approximations. The phenomenon actually being calculated in humans is more appropriately called genetic determination. This broader term connotes not only additive genetic factors but also dominance and epistasis. Formally estimating the degree of genetic determination (H) is based on the variance (V) of the differences between MZ and DZ pairs. The formula is
H = VDZ − VMZVDZ
This equation assumes, again incorrectly, that environmental influences are equivalent for MZ and DZ twin pairs. Thus, MZ twins would be expected to differ less than DZ twins for any trait having a genetic component. Variance between DZ twins should be attributed to both genetic and environmental variation; whereas variance between MZ twins should reflect only environmental variation. This dichotomy, however, can be questioned because MZ twins with monochorionic placentas should have a more common environment than MZ twins with dichorionic placentas. Only rarely is placentation taken into account.7 In conclusion, absolute heritability estimates in humans should not be accepted too rigidly; however, relative values may help identify conditions useful to pursue genetically using other methods.
GENOMIC APPROACHES TO DECIPHERING COMPLEX (POLYGENIC) DISORDERS
With the human genome being sequenced came not only identification of 21,000 human genes (the function of many of which remains unknown), but also many polymorphic DNA sequences (e.g., single nucleotide polymorphism or SNP). These polymorphisms can be exploited to identify genes or chromosomal regions responsible for a polygenic disorder. There are two general approaches – family based quantitative linkage analysis (QTL) and whole genome wide association studies (GWAS). Either is typically followed by sequencing a specific identified region of interest.
Genome wide association studies
In GWAS linkage is sought between a trait and polymorphic markers located throughout the genome. There is no hypothesis and families are not required. The approach is analogous to a case–control study. This approach is especially valuable for complex disorders the etiology of which is likely to involve multiple genes. In GWAS there are no prior assumptions as to the type of gene involved, its chromosomal location, or its action. Markers used are typically SNPs (single gene polymorphisms), previously identified in the general population and the result of an altered nucleotide compared to the general population. These polymorphisms (DNA variants) are by definition not necessarily pathological. Rather, they serve merely to localize a trait to a given chromosomal region or, ideally, gene. Subsequent studies usually are required to identify the causative genes, which may or may not be nearby. This paradigm differs from traditional approaches in that no a priori hypothesis (i.e., candidate gene) exists.
Using GWAS, progress is burgeoning for identifying genes involved in complex (polygenic/multifactorial) traits. Success has been facilitated by commercially available platforms consisting of 500,000 or more SNPs. Other types of DNA polymorphisms can be used, such as copy number variants. Caveats exist, notably the need for large sample sizes (N = 1000 controls and 1000 cases). Ethnically homogeneous samples help avoid the greatest pitfall – ethnic stratification by which differences between cases and controls connote not a disease but simply differences between ethnicities of cases and controls. Corrections must be made for multiple comparisons. Given the high likelihood of false positives, significance must be 10⁻⁶ to 10⁻⁸ to be meaningful, and preferably 10⁻18 the approach has been applied successfully for polycystic ovarian disease8 and premature ovarian failure9and endometriosis.10
Familial linkage (QTL) analysis
Chromosomal region(s) that co-segregate with a polygenic trait can also be identified through linkage analysis, preferably using multiple affected individuals in a given family.
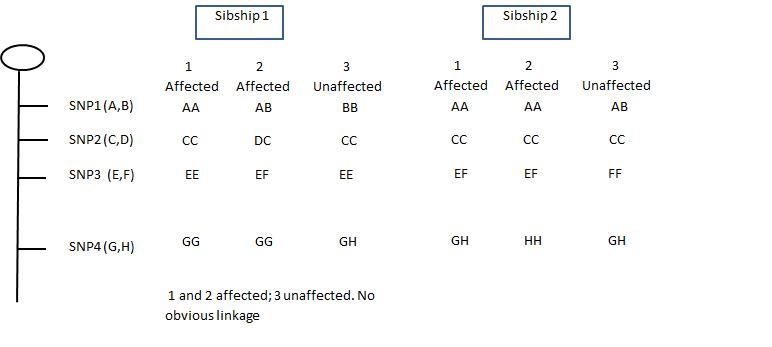
Identification of the several genes responsible for polygenic disorders requires methods such as (a) affected and unaffected sibling pair analysis; (b) multi-point linkage analysis; and (c) transmission disequilibrium studies. Figure 11 below shows idealized results in a given family in which four SNPs were analyzed in three sets of family members. Assuming all three family members have the same disorder. If all have identical SNPs, that indicates a site of potential interest. In the illustration, the chromosomal region between the SNPA and the SNPB would be worthy of further analysis. Candidate genes within the region(s) identified might be explored through a search of genome databases. Promising candidate genes can be analyzed in more detail by direct (sequencing). The goal is to detect a perturbation (deletion, frameshift, point mutation) in that gene in those individuals having the disorder in question.
Familial studies using this approach are frequently undertaken after GWAS have identified promising candidate regions. Mother, father, and affected child are often studied ("trio"). One can search multiple affected sibs to determine which SNPs are found only in affected cases.
| Fig. 11. Localizing a mutation (affected) to a specific SNP on a given chromosome. In each of the two sibships, sibs 1 and 2 have the same autosomal recessive disorder; sib3 is unaffected. In sibship 1, SNP4 remains as a candidate because both affected sibs are GG and their unaffected sib differs. In sibship 2, both SNP1 and SNP2 remain candidates but not 3 and 4. |
REFERENCES
Simpson JL, Elias SE: Genetics in Obstetrics and Gynecology, 3rd ed. Philadelphia, WB Saunders, 2007, pp. 75–81. |
|
Murphy EA, Chase GA: Principles of Genetic Counseling. Chicago, Year Book Medical Publishers, 1975 |
|
Griffiths AJF, Miller JH, Suzuki DT et al: An Introduction to Genetic Analysis, 7th ed. New York, WH Freeman, 2000 |
|
Vogel F, Motulsky AG: Human Genetics: Problems and Approaches, 3rd ed. New York, Springer-Verlag, 1997 |
|
Lynch M, Walsh B: Genetics and Analysis of Quantitative Traits. Sunderland, MA, Sinauer Associates, 1998 |
|
Wright S: The results of crosses between inbred strains of guinea pigs, differing in number of digits. Genetics 19: 537, 1931 |
|
Loos R, Beunen G, Fagard R et al: Twin studies and estimates of heritability. Lancet 357: 1445, 2001 |
|
Chen ZJ, Zhao H, He L et al: Genome-wide association study identifies susceptibility loci for polycystic ovary syndrome on chromosome 2p16.3, 2p21 and 9q33.3. Nat Genet. 2011 Jan;43(1):55-9. Epub 2010 Dec 12. |
|
Qin Y, Zhao H, Xu J et al: Association of 8q22.3 locus in Chinese Han with idiopathic premature ovarian failure (POF).Hum Mol Genet. 2011 Oct 18. |
|
Painter JN, Anderson CA, Nyholt DR et al: Genome-wide association study identifies a locus at 7p15.2 associated withendometriosis. Nat Genet. 2011 Jan;43(1):51-4. Epub 2010 Dec 12. |